A unified framework of analyzing missing data and variable selection using regularized likelihood
Abstract
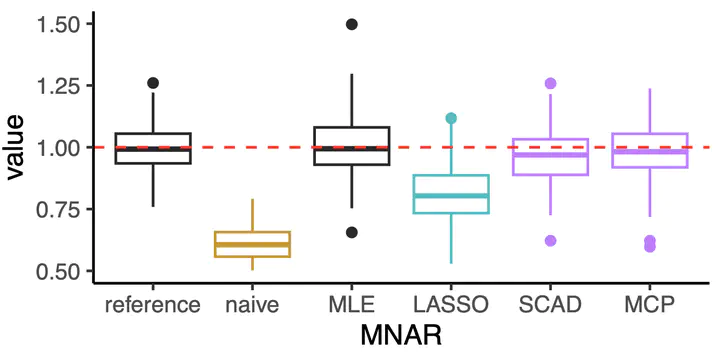
Missing data arise commonly in applications, and research on this topic has received extensive attention in the past few decades. Various inference methods have been developed under different missing data mechanisms, including missing at random and missing not at random. The assessment of a feasible missing data mechanism is, however, difficult due to the lack of validation data. The problem is further complicated by the presence of spurious variables in covariates. Focusing on missingness in the response variable, a unified modeling scheme is proposed by utilizing the parametric generalized additive model to characterize various types of missing data processes. Taking the generalized linear model to facilitate the dependence of the response on the associated covariates, the concurrent estimation and variable selection procedures are developed using regularized likelihood, and the asymptotic properties for the resultant estimators are rigorously established. The proposed methods are appealing in their flexibility and generality; they circumvent the need of assuming a particular missing data mechanism that is required by most available methods. Empirical studies demonstrate that the proposed methods result in satisfactory performance in finite sample settings. Extensions to accommodating missingness in both the response and covariates are also discussed.